水の中に赤インキを 1 滴ポツンと落とせば、やがて赤のかたまりは広がっていき、最後には液全体が一様にピンクになる。このように異物質 （液体なら溶質）がもとの物質（流体なら溶媒 ）の中に広がっていく現象を拡散という。異物質は必ず、それの濃度の小さい方へと移っていき、一様化しようとするのである。なぜそのようになるかは、経験則であるとしかいいようがない。いわゆる熱力学の第 2 法則、あるいはエントロピー増大の原理とよばれるものがこれである。このとき、異物質が均一化しようとする速さの目安として、拡散係数が定義される。


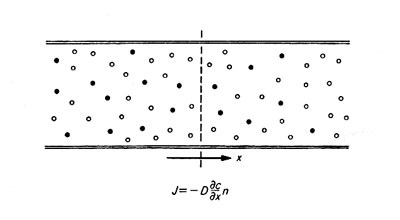
　 χ 方向に濃度勾配 －∂c/∂χ があるとしよう。 c は異物質の濃度である。 χ 方向（図の右方向 ）にいくのに従い、だんだん薄くなると仮定して、勾配にはマイナスの符号を付けておく。異物質は χ の正の方向に移動する。 χ 軸に垂直な面を考えて、この面の単位断面積を通って単位時間に移動する量を J とすれば J はこの量の密度 n に比例するから


　　J ＝ －D （∂c/∂χ）n


となる。 D は主物質と異物質（溶媒と溶質 ）とによって決まる（もちろん温度には強く依存するが ）係数であり、これを拡散係数とよび、通常 CGS 単位で表される。

∴ ［ D ］＝ cm³・s^-1

　流れる「量」というのは、質量でも分子数でもモル数でも何でもいい。元を書けば、濃度 c は比率だから ［ LMT ］ に無関係で


　　n・cm^-2・s^-1 ＝ ［ D ］cm^-1・n・cm^-3


である。つまり拡張しやすさは、長さの 2 乗を時間で割った量で表現される。


　直感的にも理解できるように、 D は温度に著しく依存し、高温ほど大きい。砂糖や塩は、湯に入れた方が、水の割合よりも速やかに混ざるのはよく知られている。


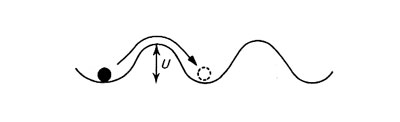
　実際には、液体の場合にはさまざまな条件が関与していて、拡散係数を表示しにくい。溶液をかき混ぜれば、たちまちに拡散は進行する。そのため、液体よりもむしろ固体中での拡散の方が詳細に研究されている。固体といえども、高温では、内部の原子は格子点を移動していくのである。その移動のメカニズムを、結晶模型を使って考えてみると、不純物原子が 1 つの格子点から山を越して隣の格子点に移る可能性はいわゆる統計力学でのボルツマン因子 exp（－U / kT） に比例すると考えられる。 k はボルツマン定数、 T は絶対温度、 U は越えるべき山の高さで、ふつう活性化エネルギーとよばれている。 U も k も 1 モル当たりに換算して、結局拡散係数 D は


　　D ＝ D_0exp（－U /RT）


となる。 D は、定数部分の D₀ と、温度依存の因子との積だと考えればいい。

　表には最初、 Na 固体中の Na 原子の拡散のように同一種類の場合が述べられている。これを自己拡散といい、実際にはアイソトープなどを用い、放射性原子を追跡するなどして拡散のありさまを調べる。


　塩素イオン Cl^- の D₀ はきわだって大きいが、このことから直ちに、 Cl^- は結晶中で動きやすい、とはいえない。活性化エネルギー U も大きく、有限温度では越えるべき山も高くなり、低温度ではむしろ動きにくくなることが多い。 D₀ の値は T → ∞ に外挿したときの定数としての意味しかない、と考えた方がいい。


　ゲルマニウムやシリコンの中の不純物を取り除く、あるいは不純物濃度を正確に決めてやることは、半導体産業においてはきわめて重要な仕事になっている。そのためこれらに混入している不純物について、 D₀ および U の値が求められている。この場合も低温では U の値が小さいほど、高温では D₀ の値が大きいほど、不純物原子は結晶中をよく動くことになる。

【理科年表編集委員会（2006年11月）】