月齢とは，朔（新月）の瞬間から数えた経過日数のことである．朔の瞬間に0.0，そこから１日たつごとに1.0，2.0と増えてゆき，つぎの朔の瞬間に再び0.0に戻る．月齢の単位は「日」であるが，明らかであるので省略されることも多い．月齢は任意の時刻について定義でき，本書に掲載されている正午月齢は，その日の正午における月齢，すなわち直前の朔からその日の正午までに何日経過したかを小数第一位まで示している．
　月齢は太陰暦や太陰太陽暦（以下，まとめて陰暦）の日付と対比させることができる．朔の瞬間を含む日を１日とする陰暦では，月齢0.0を含む日が１日，月齢1.0を含む日が２日となる．月齢と陰暦の関係は年齢と数え年の関係に似ており，月齢（年齢）は朔の時刻（誕生日）ごとに１ずつ増加，陰暦日付（数え年）は日（年）の区切りごとに１ずつ増加するものである．正午月齢は７月１日現在の満年齢に相当する概念といえるだろう（図１）．

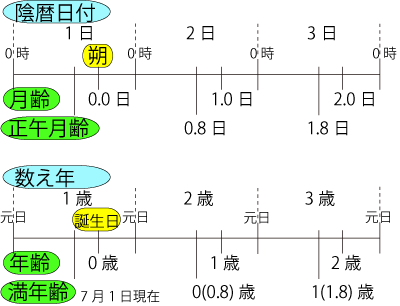
図１

　じつは月齢の登場自体も陰暦と密接に関わっている．明治５年11月に急遽太陽暦導入を宣言した明治政府は陰暦の日付も併記することで便宜を図ったのだが，その後も太陽暦の普及は思うようにはかどらず，太陰盈虚（えいきょ）１），月盈虚と少しずつ名前を変えつつも，明治42年暦まで陰暦併記が続けられていた．そして，明治43年暦においてようやく月盈虚の欄が月齢「月ノ齢朔ヨリ起算シタル日数」に置き換わったというわけである．
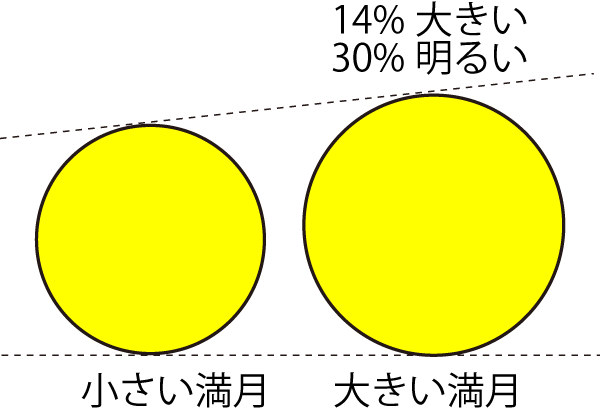
　陰暦日付が月の満ち欠けに関連しているように，月齢も月の満ち欠けに関連している．定義から月齢0.0が朔の瞬間であることは明らかであるし，平均約29.5日という満ち欠けの周期（朔望月）から，その半分の月齢14.8くらいが望（満月）の瞬間となることも見当がつくだろう．
　ただし，月齢が14.8なら必ず望になるとは限らない．これは月が地球の周りを楕円運動していることが原因である．ここで，ケプラーの第2法則によれば一定時間に月と地球を結ぶ線が描く図形の面積は等しいから，朔の状態の月から望の状態の月までに描く面積（図２の網かけ部分）の大小は経過時間の大小を示していることになる．この経過時間とはすなわち望における月齢のことであり，図２のように，月の楕円軌道と太陽の位置関係によってその大小は変化する２）．

図２

　定量的にどれくらい変化するのかを示したのが図３で，ここから望における月齢は13.9～15.6日と±１日弱もの変動があることがわかるだろう．十五夜が必ずしも満月にならない本質的な原因はここにある．

図３

　さて，ここまでの説明では1年たって地球が同じ位置に戻ってくれば，楕円軌道と太陽の位置関係が元に戻り，望における月齢の変動も一巡するように思えるだろう．しかし，実際には月の楕円軌道の向きは太陽の影響によって周期約8.85年で回転をしていることも忘れてはならない（図４）．この回転によって，たとえ地球の位置が同じであっても望における月齢は変化する．たとえば，秋分ごろの望における月齢だけをつないでみれば，その周期がはっきりと見えてくるだろう（図５）．

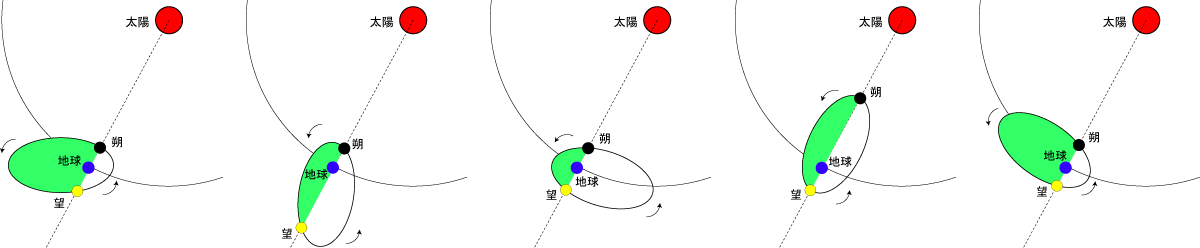
図４

図５

　この回転により，１年たって地球が同じ位置に戻ってきたときには楕円軌道も図4のような向きに回転しており，その回転分だけ先に進まないと楕円軌道と太陽の位置関係は元に戻らない．ここで，楕円軌道の向きは近地点の方向で代表できるから，近地点を基準とした公転周期である近点月（約27.55日）を考慮すればどれだけ先になるか考えることができる．具体的には，15近点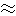14朔望月という関係が成り立ち，約14朔望月～約413日が望における月齢の変動周期ということになる．
　なお，近地点に対する公転周期は月の距離の変動周期でもあるから，望における月の距離にも同様の約14朔望月（秋分ごろのように，季節を限定すれば約8.85年）周期が見られる（図６）．ただし，一見して明らかなように両者のピークは異なっている．この違いについては，図４を見ながらそれぞれどういう状態でピークになるかを考えるとよい．距離を大きさに置き換えれば，望における月の大きさ（図７）もこの周期で変動していることがわかるだろう．

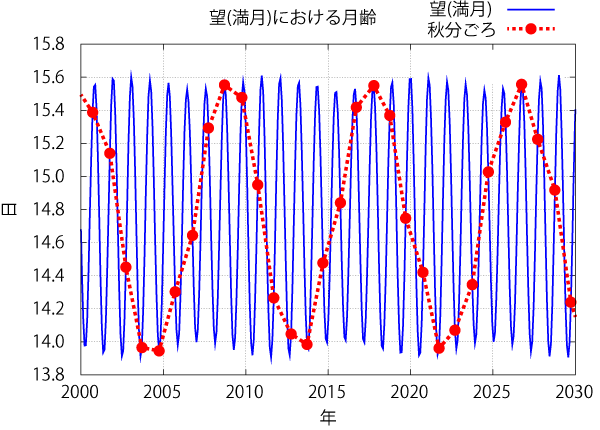
図６

図７

【 片山真人 】

１）太陰とは月，盈虚とは満ち欠けのこと．太陰盈虚という名称に変わった明治13年暦の時点で「日」という単位が記載されなくなっている．
２）面積すなわち経過時間の大小が明らかになるように，月軌道は実際よりも誇張した楕円形に描いている．
参考）暦Wiki
http://eco.mtk.nao.ac.jp/koyomi/wiki/