今、私達が使っている暦は太陽暦 （グレゴリオ暦）です。しかし、太陰暦（月の満ち欠けを基準にした暦 ）を使っている国や、日本でも明治 5 年までは太陰太陽暦を使っていました。このように国々や時代によって、異なったさまざまな暦が使用されていると、同じ日付でも暦によって別の日を指していることがあります。このような混乱を防止する目的や長い年月にわたる日数の計算を容易にするために、 ユリウス日（Julian Date ： JD）が考案されました。

　ユリウス日は紀元前 4713 年 （－4712 年）1 月 1 日正午を 0.0 とし、それから経過した日数を表わしています。つぎの日、 1 月 2 日のユリウス日は 1 です。順次、 1 日ごとに 1 を加えていくと、 2007 年 1 月 1 日のユリウス日は 245 4102 となり、時刻まで考えると 2007 年 1 月 1 日 0 時（世界時）のユリウス日は 245 4101.5 となります。ユリウス日は、太陽周期 28 年、太陰周期 19 年、インジクション（課税に関係）15 年周期がそれぞれ、第 1 年目になる紀元前 4713 年が暦元になるように決められました。つぎに、 3 周期が同時に 1 年目になるのは 3268 年です。

　最近は、ユリウス日の数値が大きいので、ユリウス日から 240 0000.5 を引いた修正ユリウス日（Modified Julian Date ： MJD）も使われています。 2007 年 1 月 1 日 0 時の修正ユリウス日は 5 4101 となります。

　 ユリウス日がわかればその日の曜日はユリウス日を 7 で割って余りが 0 なら月曜日、 1 なら火曜日、… 6 なら日曜日です。

　同様に、日の干支もユリウス日から求めることが出来ます。ユリウス日に 49 を加え 60 で割った余りを干支番号表でみると、その日の干支が求まります。たとえば、 2007 年 1 月 1 日のユリウス日は 245 4102 なので、 49 を加え 60 で割ると余りが 31 となり、干支は乙未となります。また、曜日はユリウス日を 7 で割ると余りが 0 となるので月曜日です。

干支番号表

---

 

0　甲子	10　甲戌	20　甲申	30　甲午	40　甲辰	50　甲寅
1　乙丑	11　乙亥	21　乙酉	31　乙未	41　乙巳	51　乙卯
2　丙寅	12　丙子	22　丙戌	32　丙申	42　丙午	52　丙辰
3　丁卯	13　丁丑	23　丁亥	33　丁酉	43　丁未	53　丁巳
4　戊辰	14　戊寅	24　戊子	34　戊戌	44　戊申	54　戊午
5　己巳	15　己卯	25　己丑	35　己亥	45　己酉	55　己未
6　庚午	16　庚辰	26　庚寅	36　庚子	46　庚戌	56　庚申
7　辛未	17　辛巳	27　辛卯	37　辛丑	47　辛亥	57　辛酉
8　壬申	18　壬午	28　壬辰	38　壬寅	48　壬子	58　壬戌
9　癸酉	19　癸未	29　癸巳	39　癸卯	49　癸丑	59　癸亥

　

 

表を用いたユリウス日の求め方

---

表を用いた暦日からユリウス日、逆に、ユリウス日から暦日の求め方
表を用いて、たとえば、 2007 年 7 月 15 日のユリウス日を求めてみます。

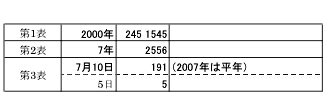合計すると 245 4297 と求まります。

逆に、ユリウス日（JD）245 4297 のグレゴリオ暦の日付を求めてみます。

2007 年は平年なので、第 3 表は平年の値を用いる。

ユリウス日 245 4297 はグレゴリオ暦 2007 年 7 月 15 日となります。 第 3 表は閏年で値が異なるので、注意が必要です。

 

 

紀元前のユリウス日の計算

---

　 理科年表の表を使って、紀元前のユリウス日を計算するときは注意が必要です。紀元前の年代の数え方は紀元元年の前年を 0 年とする規約によるので、紀元元年の前年を紀元前 1 年とする通常の方法と 1 年の差があります。紀元前 4713 年は －4712 年となります。また、第 2 表の年代はつねに正の年で使用します。たとえば、紀元前 45 年 ( －44 年 ) 1 月 1 日のユリウス日を求める場合、 －44 年は －100 年から 56 年後と考えて第 1 表、 2 表を用います。

 

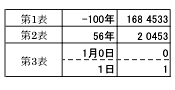合計すると紀元前 45 年 ( －44 年 ) 1 月 1 日のユリウス日は 170 4987 と求まります。
逆に、ユリウス日 ( JD ) 170 4987 のユリウス暦の日付を求める場合は

－100 ＋ 56 は －44 年で、残りは 1 だから、ユリウス日 170 4987 は －44 年（紀元前 45 年）1 月 1 日 となります。　ユリウス暦の閏の規則によれば、 －44 年（紀元前 45 年）は 4 で割り切れるので閏年です。

　

ユリウス暦、グレゴリオ暦両方の暦の対応

---

　 理科年表第 1 表は、紀元 1599 年以前はユリウス暦、 1600 年以後はグレゴリオ暦に対応しています。しかし、 1582 年にグレゴリオ暦を採用した国もありましたが、宗教的な理由その他により 1900 年代までユリウス暦を使用していた国もありました。そのため 1500 年から 1999 年までのユリウス暦、グレゴリオ暦両方に対応するためには第1表の値の代わりに、下記の値を用いればユリウス日が求まります。

年	ユリウス暦用	グレゴリオ暦用
1500	226 8933	226 8923
1600	230 5458	230 5448
1700	234 1983	234 1972
1800	237 8508	237 8496
1900	241 5033	241 5020

ユリウス暦の 1582 年 10 月 4 日のユリウス日は

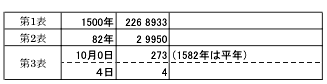合計すると 229 9160 となります。

グレゴリオ暦の 1582 年 10 月 15 日のユリウス日は、上で述べたグレゴリオ暦用の値から

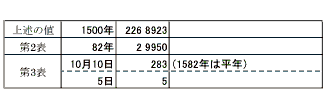合計すると 229 9161 と求まります。

 

　1582 年グレゴリオ暦の改暦では、「ユリウス暦の 10 月 4 日の翌日を、グレゴリオ暦の 10 月 15 日とする」ことでした。確かに、ユリウス暦 10 月 4 日（ユリウス日 229 9160）のつぎの日 229 9161 がグレゴリオ暦の 10 月 15 日 となっています。 ユリウス暦 1582 年 10 月 4 日のユリウス日（229 9160 ）を 7 で割ると余が 3 で、曜日は木曜日、グレゴリオ暦 10 月 15 日のユリウス日（229 9161）を 7 で割ると余が 4 で、曜日は金曜日となります。日付は 10 日飛ばしましたが曜日は連続しています。

【中井　宏　国立天文台天文情報センター（2006年11月）】

 

関連記事：「ユリウス暦とグレゴリオ暦」

【 参考文献 】
青木信仰 ：『時と暦』、東京大学出版会（1982 ）